Jonathan Dobres

The algorithm above is a variant of one that currently runs on my front page. The heart of it is a circle packing algorithm, which you can find at my GitHub. All the code is there, so I won’t bother to explain every line of it here. There are, however, a few interesting bits I’d like to highlight.

Circle Packing

Circle packing is a well-established topic in mathematics. The central question is: how best can you cram non-overlapping circles into some available space? There are lots of variations on the idea, and lots of ways to implement solutions. My version works by proposing random locations for circles of smaller and smaller sizes, keeping only the circles that do not overlap with any circles already on the canvas. In pseudo-code, the simplest method looks like this:

let existing_circles = [ ]
let radius = 100

while (radius >= 0.5) {
  trying 1000 times {
	let new_circle = circle(random_x, random_y, radius)
	if (new_circle does not overlap existing_circles) {
	  add new_circle to existing_circles
	  restart trying
	}
  }

  // If we made it through all 1,000 tries without placing a circle, shrink the radius by 1%.
  // The program stops if the radius drops below 0.5 pixels.
  radius = radius * 0.99
}

The above is pseudo-code, and it hides a lot of complexity. In particular, line 7—new_circle does not overlap existing_circles—glosses over the most interesting part of the algorithm. What, exactly, is the most efficient way of checking to see if a new circle does not overlap any of the ones that have already been placed?

Notice that existing_circles is just a list, and it stores circles in the order in which they were created. Every time a new circle is proposed, its position is compared to the first circle in the list, then the next, and so on, up until a comparison fails or the list ends. On the one hand, the list structure has an implicit optimization: larger circles were created first and will be checked first, so areas on the canvas with the highest potential for overlap get checked early. On the other hand, if our maximum circle size is smaller, this advantage disappears. And in either case, successfully placing a new circle means that every existing circle needs to be checked, every time. The more circles we’ve placed, the more will need to be checked. This is like looking up the definition of the word packing by opening up the dictionary to the first entry and dutifully reading every word from aardvark to pace.

For the purposes of my website, that’s not acceptable—I need something that fills the canvas pretty quickly.¹ What we really need is a data structure that organizes circles by their position, at least vaguely. That would make it easy to restrict our comparison only to circles that are near to the proposed new circle. Enter quadtrees.

Quadtrees

Of course, if you were looking for a specific word in a dictionary, you wouldn’t read it through from the start. Searching for packing, you’d probably grab a big chunk of the pages and flip open to somewhere near marzipan. Knowing that p comes after m, you flip forward by another chunk, landing at quintessence. Having gone too far, you browse backwards, perhaps more carefully, until you arrive at packing. This method of searching the dictionary is, roughly, a binary search. Rather than starting at the beginning of the data, you jump straight to the middle. If that’s not the object you’re looking for, go halfway to the beginning or end, depending on whether you’ve overshot or undershot. Continue taking these ever-smaller half-steps until you’ve narrowed your search to the thing you’re looking for.

This method of searching is a little less efficient for words near the beginning of the dictionary, but much more efficient, on average, across all possible entries.²

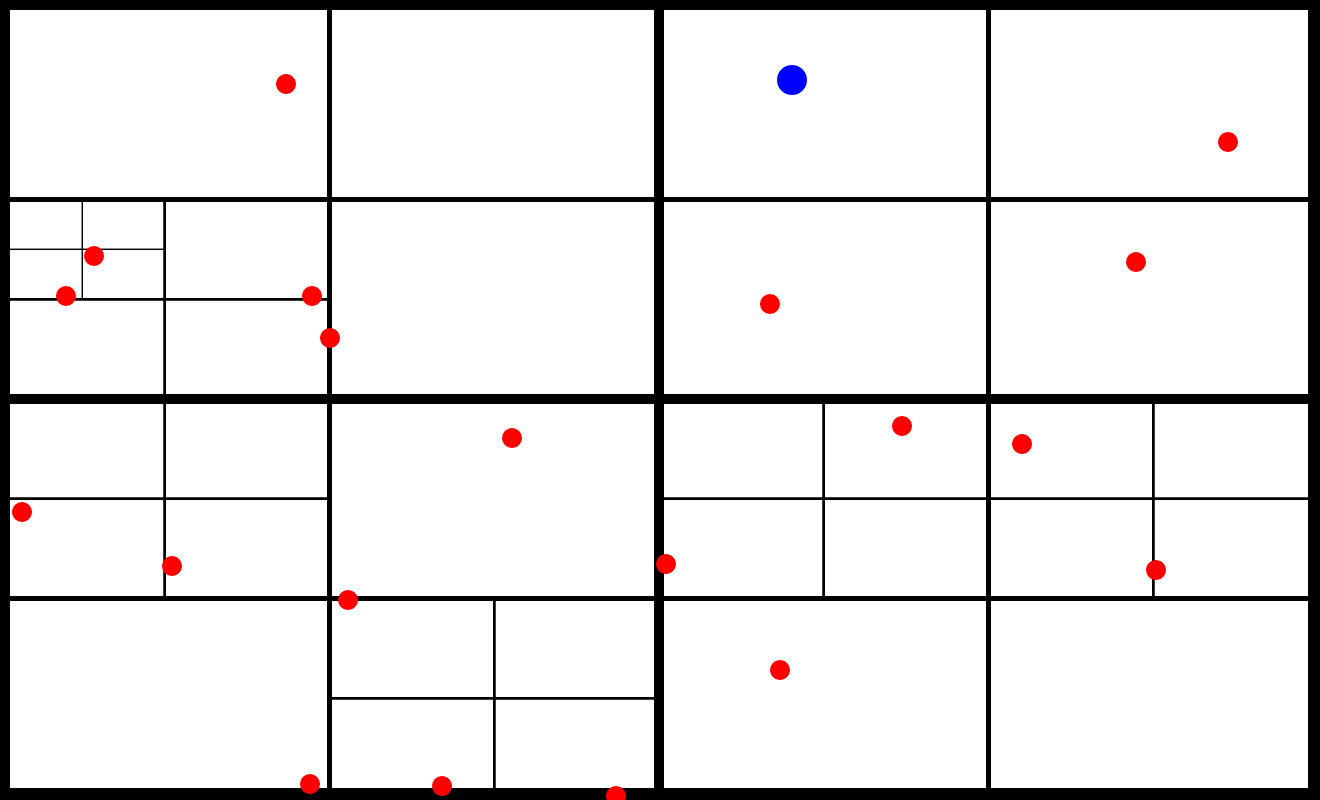
A quadtree generalizes this idea to 2D space, like our canvas. The quadtree works by dividing the canvas into four quadrants. Every time we propose a new circle, the quadtree checks to see where the circle landed. If the circle lands in an empty cell, great, make a note of that. If the circle lands in a cell that already has a circle, the cell splits into four smaller cells, repeating until each cell once again holds one circle. The image above shows a quadtree storing twenty circles, with a twenty-first proposed circle in blue. When checking for possible overlaps, we can quickly determine that three of the four biggest quadrants don’t overlap the proposed circle and one does—four quick checks and we’ve eliminated 75% of the canvas, no need to check the seventeen circles contained within. The proposed circle does overlap the upper-right quadrant, so its sub-quads will need to be checked—four more checks. After about eight comparisons, as opposed to twenty, we’ve determined that the proposed circle is valid. As more circles are added and the grid becomes finer, the number of checks becomes roughly proportional to the potential area of overlap.³

There are many fine implementations of quadtrees, and I certainly don’t claim that mine is the best, but it was very satisfying to learn it myself.⁴

Into the Quadforest

I’m glossing over one other thing. We don’t just want to compare the circle positions, but rather, their areas. Using a single quadtree, we have to assume that the potential search area is a square with side lengths equal to the diameter of the proposed new circle, plus the maximum circle diameter stored in the tree. In practice, as the circles get smaller, we’ll be checking a much bigger area, and many more circles, than is necessary. The solution is to use multiple quadtrees, the first of which stores and searches against the largest circles, the next smaller ones, and so on. In this way, we can ensure that larger circles are checked first, restoring the advantage from the naive method.

All these optimizations really do make a difference. When the maximum circle size is large (say 200 pixels in diameter), the quadforest search is about three times faster than the naive list search. When the maximum circle size is smaller (say 20 pixels in diameter), the quadforest is about thirty times faster. Code that pits the two methods against each other in a race is available in the repo.

Happy Accidents

Having gotten the algorithm working nicely, I wanted some visual interest, or as the kids say, “art”. My first thought was to have the circles pop into existence with an animation. I’m not clearing the canvas on each new frame, which saves me from having to redraw every circle for every frame. And because I was testing my quadtree, the drawing commands were set to draw unfilled, outline shapes. So when I specified a five-frame “pop” animation, what I ended up with was five concentric rings for each circle—the ghosts of the pop animation. These appear thin and delicate for the larger circles, but thicker and almost solid for the smaller ones. The unexpected patterning produces a variety of texture and brightness that I really enjoy.

And there you have it. Efficient random circle packing, done fast, live, and pretty. The code for this algorithm is available on Github.