Jonathan Dobres

Let’s say you find yourself in a small, quiet room. The only point of interest in this room is the southern wall, upon which there are three light switches, all in the off position. One of these three switches operates a table lamp in a room located on the other side of the building. You can leave the switch room to go examine the lamp, but if you do, the door to the switch room closes forever. You can’t see, hear, or otherwise perceive the state of the lamp from the switch room. So, using nothing but these three light switches and your one trip out of the room, tell me which switch controls the lamp.

There’s enough information in the above paragraph to solve the problem, I promise (I’ll reveal the solution at the end of this post). Solving the problem requires you to think about it in a new, unusual way. If you want to win, you have to think outside the box. Take an intuitive leap. Think different. Shift the paradigm. Do some lateral thinking. You can describe this type of problem with whichever cliché you like best, but a psychologist would call it an “insight problem”.

An insight problem is fundamentally different from, say, an algebraic equation, a Sudoku, or a Rubik’s Cube. No matter how tricky the math looks, how many numbers are missing from the Sudoku grid, or how long the Cube has been sitting in a disused desk drawer in your attic, you can solve these puzzles. Given a complete understanding of the rules and enough time, a solution is inevitable. Insight problems, on the other hand, carry no such guarantee. If you can’t think creatively, you can’t solve the problem, and perhaps you never will.

The requirements of insight problems are different from those of non-insight problems. It should come as no surprise to you, then, that the feeling of solving an insight problem is different as well. This was studied back in the late ’80s. Researchers gave subjects sets of problems to complete, and asked them to rate how close they felt they were to the solution every fifteen seconds. Ratings for non-insight problems followed a predictable pattern; as subjects got closer to the solutions, they felt like they were getting closer. But the insight problems were different. As subjects chewed on the insight problems, their ratings never budged, until the moment the solution came to them. The subjects felt as if they were treading water, turning the problem over and over again in their minds, and then suddenly—bang, boom, eureka!—something clicked, and all at once the solution was obvious.

I can’t help but think of the recently released Portal 2 and its predecessor, Portal, as the world’s most successful insight experiments. Before I get into why, let’s take care of the preliminaries. Portal is a perfect video game (and Portal 2 is a near-perfect successor). I don’t say that often, but it’s true. As a game, as a story, and as an interactive experience, Portal lacks for nothing. It is thrilling every step of the way and sticks around for exactly the right amount of time. If you haven’t played it yet, you should buy it right now. It costs a measly ten dollars.

Portal is a puzzle game. The goal of each puzzle is to get from the entrance of each testing chamber to its exit. Your only tool is the Aperture Science Handheld Portal Device, a gun-like object that does one thing: creates a wormhole linking any two flat surfaces. If you’ve never played Portal, this video from an earlier version of the game is worth a thousand words.

With the portal gun in your hand, everything you’ve ever learned about moving through your environment, about the laws of physics, is suddenly open to negotiation. The portal gun breaks your assumptions about how the world works and gives you abilities you can only discover through experimentation. The point is this: playing Portal requires insight.

This stands in stark contrast to just about every other video game ever made.Games like Halo and Call of Duty may be dressed in fancy clothes, but really, all you have to do is murder your way to victory. In _Mass Effect 2, _an excellent game set apart by its top-notch writing and expansive atmosphere, you murder your way to the next dialogue tree. I’m not saying that you don’t need skill to play these games, or that you can’t play them creatively, but they require the sort of skill and creativity you’d employ to solve a particularly hard math problem, with guns.

There are other types of games, of course, games like Sam & Max or Curse of Monkey Island, that require a fair bit of creative thinking, but the creativity here is oddly constrained. It’s all about figuring out which quirky item from your quirky inventory you need to use on some oddly specific (quirky) part of the quirky world to progress to the next quirky set piece. So whether you’re playing Bioshock or Day of the Tentacle, the rules are clear, the win condition is readily apparent, and victory is, in a sense, inevitable.

Portal is an entirely different beast. There are no health meters, no command menus, no inventory screens, no neatly written mission objectives, and no hint system. You have one weapon, and it does exactly one thing; the game is all in how you use it. In most testing chambers you can see your goal from the very start. The only question is how you’re going to get there, and the only way to answer that question is to explore the chamber. So, you start looking around. You move through the chamber, perhaps taking note of which surfaces are portal-compatible and which aren’t. You might notice that there’s a button that needs pressing on the floor over here, and over yonder, on the other side of a bottomless pit, a big weighted box that could be placed on top of it. But how do you unite the box and the button? With your trusty portal gun, obviously.

Obviously. All you have to do is use the portal gun to…

Obviously…no, that won’t work. Maybe if you put one portal on this wall, and the other on the floor…

Obviously? No, clearly not. Alright, let’s see how things look when you portal yourself over to the box and…nope.

Obviously this is impossible. Who the hell designed this thing? This test chamber is unsolvable. You’d need an extra box, or another way to press the big button. But to do that you’d need to figure out some way to simultaneously get both of the…

Oh.

Oh!

And just like that—bang, boom, eureka!—the solution becomes obvious, all in a flash of insight.

The only thing harder than solving an insight problem is creating one for someone else to solve. You have to provide just enough information to make the problem solvable, but not so much that the problem becomes too easy or straightforward. Insight problems are very experiential. As I said earlier, solving them feels different from normal problem-solving. Unbelievably, the fine folks at Valve Software have created a game that generates the insight experience, that undefinable eureka feeling, over and over again (that Valve accomplishes this by meticulously testing and quantifying player behavior is another feat in and of itself). Forget Portal’s pitch perfect dark humor, its strangely immersive storytelling, or the wonderful look of the game. Portal, as a game, is about capturing that moment of insight. The reward the player receives for solving each test chamber is transient, unique, powerful, and entirely internal. No other game has ever offered something this pure to the player. No other game triggers this sort of feeling in the player’s brain. This, I believe, is what has made the Portal series such a wild success.

In closing, let’s return to our hypothetical light switch room. Using just these three switches and a single trip outside to check on the lamp, how can you tell which switch is the right one? Let’s label the switches A, B, and C for convenience. Turn on switches A and B. Now wait fifteen minutes or so. Turn off switch B. Congratulations, you’ve just solved the problem. Exit the switch room and go examine the lamp. If the light is still on, then obviously switch A is the right one. If the light is off, feel the bulb. Is it hot? If so, then switch B, which powered the lamp for fifteen minutes, is the right one. Finally, if the bulb is cold that means its switch wasn’t turned on at all, so switch C is the correct answer.

Update: Several alert readers have pointed out that my snowfall total for 2011 doesn’t seem to match other prominent reports. To double check myself, I downloaded the newest data set available from the Utah University Climate Center. To my surprise, the snowfall total is now dramatically larger. My previous data set was downloaded only about a month ago. I’m not sure why the snowfall totals would have been so inaccurate. Perhaps certain measurements lag behind more than others. In any event, my thanks go out to my commenters.

The annual snowfall plot has been amended (other plots were not changed by the update), and parts of the post have been rewritten to reflect the update.

We Bostonians have a lot of pride. Our pride runs the gamut from our sports teams to our collective intellectual superiority. More than anything, though, we’re proud of our weather, or rather, our ability to survive it. That doesn’t mean that we don’t love to bitch and moan about how horrible it is, every single year.

The winter of 2011 was widely regarded as one of the worst this nation has ever faced. At one point, snow covered portions of 49 out of 50 states. Boston was no exception. Desperate to reduce the burden created by the accumulation of tons and tons of unmelting snow, a state senator at one point suggested that we dump our excess snow into Boston Harbor.

This winter was a bad one, certainly. But as the temperatures rose and the banks of snow finally started to melt away, I got to wondering: How bad, exactly? Where does this winter rank in the history of Boston’s winters, and what, specifically, made it so unusually harsh? Being a scientific sort of guy, I’ve taken it upon myself to examine these and a few other questions about Boston’s weather patterns.

Enormous, Italicized, Electroluminescent, Mile High Disclaimer

Climatology is very complicated. I am not now, nor have I ever been, a climatologist. I’m just a guy with a background in the scientific method, an obsession with the crunching of numbers, and a knack for presenting the results. What follows is a fun project I wanted to do. Don’t take the results as gospel.

About the Data

The analysis presented here is based on freely-available data from the Utah State University Climate Center. The specific data used come from two weather stations. Data from 1920 through the present come from the NOAA weather station at Logan Airport (FYI, the weather station appears to predate the airport). Data prior to 1920 come from another weather station that was located just off of Boston Common, which operated until 1935.

The fifteen year overlap in the operations of the two stations allowed me to compare their measurements day-to-day, and they are in nearly perfect agreement. Therefore I’ve combined the data into a single set that spans a period of just under 118 years, from 1893 to now. Put another way, that’s weather data for the last 43,114 days. I could have gotten a few more years of historical data by incorporating readings from stations in Boston’s outlying suburbs, but the few extra years I’d gain from this didn’t seem worth the potential disadvantages of incorporating data from outside the urban microclimate.

Data were analyzed and plots were created with R and that hot new kid on the block, the instantly indispensable RStudio.

The Winter

Bostonians react to the news of an oncoming December storm with the sort of conduct usually reserved for an Apocalypse. We swarm the nearest supermarket and pick it clean of chicken, bread, eggs, milk, and rock salt, as if it’s just been announced that the rotation of the Earth is going to grind to a halt and trap us in an eternal, frozen night. We love the drama and pretend to panic, sure, but nobody’s really surprised to see that first December snowfall. On the other hand, we’re always shocked—shocked—to see a snow storm in March. That’s a little strange, given how the numbers stack up:

Unsurprisingly, Boston receives the bulk of its snowfall in January and February, just over a foot per month. The city also gets just under eight inches of snow in both December and March. It’s interesting that we tend to think that December is snowier than March, but in reality, they receive equal amounts of snow.¹

Small amounts of “freak” snow can occur at almost any time of year. For instance, just shy of an inch fell on May 8^th, 1938. The Junes of 1952 and 1992 somehow saw trace amounts of snow as well. The only month of the year in which snow has never been recorded is, somewhat surprisingly, September.

On the other end of the scale, the single snowiest day in Boston was fairly recent: February 17^th, 2003, on which we received 23.6 inches. The second runner-up is—laugh with me now—April Fool’s Day of 1997 (22.4 inches). Third on the list is January 20^th, 1978 (21.0 inches). Oddly enough, this is not the legendary Blizzard of ‘78, which didn’t hit Boston until about two weeks later, on February 6^th. That storm deposited 27.1 inches of snow over the course of two days, and was at the time a record-breaker. You have to go back twenty more years, to February 16^th, 1958 (19.3 inches) to find the next-highest snowfall. As for our easiest winter, the medal goes to 1937, during which Boston received just a bit over nine inches. It was also the sixth-warmest winter on record, with an average temperature of 35.2 degrees.² That must have been nice.

But let’s get back to the present. How does the winter of 2011 stack up against history?³ The average temperature was 29.9 degrees 30.2 degrees, which is about average. It snowed on 19 separate days, which is also average which is a little more frequent than usual.⁴ We did, however, receive almost a foot more snow than is normal about twice our normal annual snowfall (thank you again, to the commenters who got me to double check my data source):

This was surprising to me. The snowfall total is certainly above average, but not as high as I would have thought, especially in light of how terrible this winter felt. So given the fairly average temperature, average snow frequency, and non-catastrophic snowfall total (relative to, for instance, 1996 and 1994), what made this winter feel so unendingly, mercilessly awful?

Boston got absolutely hammered this winter, receiving nearly 80 inches of snow, making it the eighth-snowiest winter on record. But there’s something highly unusual about this winter that made it even more brutal.

This plot represents the number of days in each winter with a high temperature above freezing.⁵ In other words, the number of days on which snow could thaw. As you can see, the winter of 2011 was very unusual. Temperatures never dipped all that low, but neither did they manage to climb above freezing very often. All told, Boston had about two weeks fewer thaw days than it usually does.

Such a low number of thaw days is quite rare. This, I think, is what really made this winter so bad. It snowed, and then the snow stayed. Twelve inches of snow might make for a bad commute, but if it hits 50 degrees the next day, it isn’t really a long-term problem. If, however, the twelve inches sit on the ground until another eight inches comes along and turns it into a mountain of twenty, that’s a problem. Landlords get lazy about shoveling. Pedestrians tire of trudging through the increasingly treacherous sidewalks. Politicians go snow mad and start to talk of dumping it all into the harbor or melting it down with flamethrowers.

Climate Change

We’ve been hearing a lot about climate change over the last few years, thanks in no small part to Vice President Al Gore. Perhaps you’ve seen his movie, or read his book, or his other book. I don’t mean to sound sarcastic here. The signs of man-made climate change are varied and pervasive. Converging streams of evidence from diverse fields of science all strongly indicate that the planet’s average temperature has been rising gradually since the Industrial Revolution. Since my data just happen to start at the beginning of industrialization, I wondered if my simple measurements would show any evidence of a warming trend.

Why yes, they do. The orange line in this plot is a simple linear regression through Boston’s average annual temperature.⁶ The slope of the regression is statistically significant (p < .0001), or in English, temperatures do appear to be climbing steadily upwards, much more so than you’d expect from random fluctuations. The data indicate that since 1893, Boston’s average temperature has increased 2.3 degrees. 2010 was objectively the hottest year on record for the city.

It’s also worth noting that Boston now gets about twice as many days above 90 degrees per year as it did at the turn of the last century. In the first twenty years of the data (1893 - 1912), Boston had an average of six days per year above 90 degrees. In the most recent twenty years (1991 - 2010), Boston had an average of eleven. The same statistically significant, upward trend is also apparent:

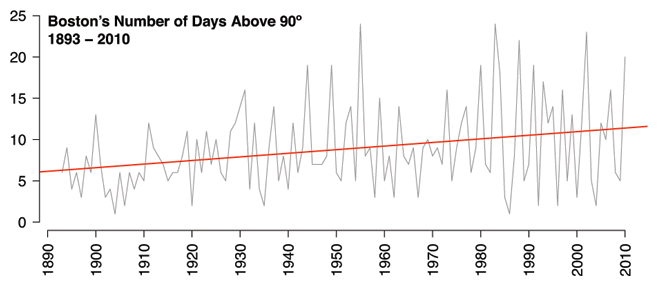An Inconvenient Truth was produced shortly after Hurricane Katrina hit New Orleans, and so Mr. Gore took care to point out that warmer temperatures put more moisture in the atmosphere, which ultimately produces more powerful storms. So, if Boston is getting warmer, might we see a comparable increase in annual rainfall?

Yup. Once again, the regression line is significant (p = .001), indicating that rainfall totals have been steadily increasing over the years. Boston gets about seven more inches of rain now than it did in 1893, which is pretty striking, since an inch of rain contains a lot more moisture than an inch of snow (I’ve heard that an inch of rain works out to about a foot of snow).

Looking at this plot, you can see that the 1950s were bizarrely wet. In fact, the four wettest years in the data set are all from the ’50s. The wettest year is 1954 (62.5 inches), during which Boston was battered by two hurricanes, Carol and Edna, in rapid succession. Next on the list is 1958, which is a bit of a mystery. The only hurricane of note for the United States that year was Hurricane Helene, but it didn’t cause much trouble for Boston. There were, however, two unusually strong storms at the very end of winter. Here’s an actual NOAA report on the matter dating from 1958. The single wettest day on record is August 19^th, 1955, during which the city was pelted with just over seven inches of rain. This was the worst day of Hurricane Diane’s Boston tour, which loosed a total of 12.4 inches of rain over the course of three days.

In short, we can conclude that Boston is both warmer and wetter than it was a century ago, with no sign of slowing down. As if to add insult to injury, it appears that the increases in temperature and rainfall have had no real effect on annual snowfall. If anything, annual snowfall totals have trended slightly upward in recent years, albeit not significantly.

Concluding Remarks

So, what have we learned today?

The winter of 2011, the awfulness of which prompted me to seek these data in the first place, was awful in a highly unusual way. Sure, it was snowier than average, but that wasn’t the real problem. This winter was an extremely snowy one, albeit not unusually cold. Rather, temperatures hovered in a small, frustrating range that deprived the city of about two weeks’ worth of thaw weather. That lack of melt made a world of difference.

Speaking of worlds, climate change is real. Even my amateurish, admittedly clunky analyses makes that glaringly obvious. Boston’s temperatures are on the rise and we’re getting heavier rain. In a coastal city where most of the architecture predates the invention of air conditioning, these findings should prompt serious concern. My analysis is mostly in agreement with more official climate reports.

If you poke around and look for the record highs and lows, it becomes obvious that one should never confuse an isolated hot or cold spell for the slow moving, long-term effects of climate change. The coldest day ever recorded in the city was February 9^th, 1934, which hit a bone-chilling low of -18 degrees. Conversely, the hottest day on record occurred way back on July 4^th, 1911, when thermometers reached a scorching 104 degrees. This corresponds to a historic heatwave that killed 380 people throughout the Northeast.

Lastly, I’d like to point out that this analysis was generated from freely-available data, analyzed with a freely-available programming environment, and presented to you on a freely-available blogging platform. Anyone could have done what I’ve done here, given sufficient knowledge and motivation. If you lack sufficient knowledge and motivation, but still want to explore the data, WeatherSpark has you covered (though their Boston data only goes back to 1948, amateurs).

2011 may have been a bad year for winters, but as far as freedom of information goes, it’s a pretty interesting year to be alive.

While wandering around PAX East’s gargantuan Expo Hall, I found myself inexplicably drawn, over and over, to the Chessex booth. This is a company whose sole product is dice. Don’t be fooled by their awful website, these people are serious about their product. The booth was bordered by bin after bin of dice, meticulously arranged by color and number of sides. They had dice of every hue, material, size, and shape you could possibly imagine, and many that you couldn’t. I picked up a set of 6-sided dice labeled in Roman numerals for the Tall One, as well an odd pair whose sides were labeled as noun/verb/adjective and who/what/when/where/why/how. On dice! Also one with some mathematical symbols on it. And two 6-sided dice that I just really, really liked the look of. It was at this point that I finally managed to wrench myself from Chessex’s candy-colored grasp, gazing in wonder at the hive-like activity of nerds picking out dice, like bees pollinating a field of flowers.

Did I need these dice? No, of course not, but that’s hardly the point, and at about 50 cents apiece, it’s not like I’m risking a plunge into massive dice debt. My recent purchases have, however, gotten me thinking about dice and basic probability. Given a roll of two dice, how likely are you to get a particular value? What patterns do these numbers obey? Just how lucky is 7? If the guy running an RPG tells you that you need “a 6 or better” to win this encounter, just how easy or hard is that? I’m not an expert in probability or even a mathematician, but I thought it’d be fun to investigate these questions. Dice and data come from the same Latin root, after all.

I can remember playing a board game with my dad, maybe Monopoly, maybe Parcheesi, where he decided to drop some Dad Knowledge on me: 7 is the most common roll of the dice. Roll one die, and no matter what number comes up, there’s going to be a number on the second die that can make the two sum up to 7. This is not true of any other combined roll. If I’m trying to roll a 6, for whatever reason, and 6 comes up on the first die, I’m guaranteed to overshoot. So, given a pair of 6-sided dice, 7 is the most common roll. But how common? If I were a proper mathematician, I’d squint really hard and pull an elegant formula from the depths of my brain. But I’m a psychologist and statistician, and increasingly, we prefer R. So I’ve used R to simulate one million rolls of a pair of 6-sided dice. Here’s the resulting distribution of rolls:

It turns out that these rolls follow a perfectly triangular distribution. I can already hear the statisticians in the audience furrowing their brows, and no, these numbers do not follow the more common normal distribution. The odds do not follow a bell curve, but rather, your odds of rolling a particular number decrease linearly from the peak of 7. This is true of all two-dice rolls, and if you don’t believe me, here’s a simulation of two 20-sided dice:

Boom. Triangle. Based on these simulations, we can extrapolate some rules for the probability of rolling a particular number. Given a pair of n-sided dice, the most common roll will be n + 1. The odds of this roll are 1/n. The odds of the other rolls decrease linearly as you move away from the peak, bottoming out at a probability of 1/n² at the ends. So using a set of 6-sided dice, the most common roll, 7, has a one in six chance of being rolled. Rolls of 2 or 12 have just a one in thirty-six chance of appearing.

The statisticians in the audience are probably starting to feel a longing for their beloved normal distribution. Luckily for them, the distribution of possible values starts to approximate a normal distribution as more dice are added. Here’s the simulation for one million rolls of three 6-sided dice:

This is definitely the familiar bell curve, albeit a slightly platykurtic one. Great word, right? Platykurtic. It means that the peak is slightly flatter than you’d expect compared with a perfect bell curve.

One last thing. I’ve often played tabletop games where I’m told that I need to roll some number or better, for instance, “You need a 7 or better to win this encounter.” Based on the distributions we’ve covered so far, it’s a simple matter to transform them into game-appropriate cumulative functions:

You have a 100% chance of rolling a 2 or better (duh), whereas you have just a 3% chance of rolling a 12. The curve is nonlinear, a fact which I doubt most DMs ever keep in mind. So if I’m the DM and I want my party to have a 50/50 chance of winning the battle using their 6-sided dice, the roll they need is 7.5 or better. Obviously that’s not possible, so the real question is whether I want the roll to be slightly easier (7 or better) or slightly harder (8 or better). What I find interesting is that 8 feels like a fairly high roll, but in fact, you’ll roll an 8 or better 42% of the time.

If you’re rolling a single die the odds of getting any particular number are uniform, assuming the die is fair. But the minute you start messing around with multiple dice, the underlying distribution changes and begins to approximate the probabilities of real-world statistics. The more you know, right?

In 1961, newly elected FCC chairman Newton N. Minow (actual name) famously declared that television was a “vast wasteland”. Minow believed that television had the potential to be something truly great, but then, as now, it was too full of superficial, meaningless garbage and grating, obnoxious advertisements.

Fifty years after Minow’s speech, I couldn’t help but think of him as I toured the exhibition floor of the Penny Arcade Expo and evaluated the plethora of 3D technology on display. I might be misremembering last year’s PAX, but it seemed like the only 3D technology on the floor then was a small section of NVIDIA’s booth, a timid, tentative offering that nevertheless managed to draw a perpetual crowd. This year, NVIDIA was pushing 3D as hard as it could. Its booth—more accurately described as a small mall of game technology, such was its size and layout—was dominated by 3D. The booth was fronted by a 3D-capable monitor 103 inches in size. Passersby could pick up any one of a dozen 3D glasses to experience the effect for themselves.

That experience, I’m sorry to say, is disappointing. It’s not that it doesn’t work; I’m practically stereoblind, and even I was able to perceive some depth in the displays. But just because a thing works, that doesn’t mean that it’s worth your time. 3D projection is taxing on two fronts: it requires a variety of technological trade-offs to work properly, and makes unusual, often uncomfortable demands of an observer’s visual system.

The biggest trade-off is brightness. One way or another, the 3D setup has to send two separate images to each of your eyes. This means that the image is going to look, at best, half as bright as it would under 2D viewing conditions. This may be acceptable in a movie theater, where you’re sitting in front of a massive screen that pours tons of light into an otherwise completely dark environment, but it’s terrible in the context of a living room or a show floor. With my 3D glasses on, screen images appeared dismally murky. Details were lost and some scenes became entirely unintelligible. The goggles felt awkward to wear, especially over my eyeglasses. In short, it’s an uncomfortable viewing experience of questionable value, to say nothing of the cost of the technology. No person is in his right mind would spend the hundreds, possibly even thousands, of dollars necessary to play a 3D game in his own home.

One intriguing alternative is Nintendo’s 3DS, which uses a variation of the “hologram” cards that were popular in the 80s (you know, hold it at one angle, you see one picture, hold it at a different angle, you see another). When you hold the 3DS at just the right angle, the screen beams two separate images into each eye, creating a depth percept without the need for expensive monitors or dim glasses. The image is bright, and lining yourself up is simple. That the effect works at all is extremely impressive, but I still question the practically. If you’re like me, you move around when you play games, and if you move the 3DS out of its narrow “sweet spot,” you’ll get a double image instead of 3D. Though promising, it’s worth keeping in mind that this method will only work with a handheld system, and cannot be adapted for a television.

Now let’s talk vision science. For the record, what I have to say here applies to 3D movies as well. 3D projection is not natural, or as we might say in the lab, it’s not ecologically valid. The human eye regularly performs two related but independent actions: convergence and focus. Hold up a finger at arm’s length, then move it toward your face. As you keep your eyes on your finger, you’ll notice two things. One, your surroundings will fall out of focus as your finger gets closer to your face. Two, your eyes might start to feel weird. This is because they’re converging at a fairly extreme angle. Essentially, you’re crossing your eyes. Out in the real world, focus and convergence always change in tandem. But in a 3D movie or game, your point of focus is constant (the screen), while convergence changes depending on the contents of the scene. I don’t suppose you’ve seen the trailer for Pirates of theCaribbean 4? The trailer is in 3D, and like most trailers, it cuts rapidly from shot to shot. The depth plane changes every few seconds, and it’s completely exhausting. The human visual system simply isn’t built to process the world this way.

3D suffers from artistic problems, too. Designers and directors have had over a hundred years to learn how light, color, texture, and spatial arrangement affect a scene. We have no such body of knowledge for the manipulation of depth (da Vinci and Picasso notwithstanding). Nobody designing 3D games, or directing 3D movies, really knows how to use 3D effectively. I watched someone play World of Warcraft in 3D for about fifteen minutes. Every time he killed a monster, a large notification would float over the screen at the front of the depth plane, obstructing the ongoing action. The effect was distracting and ugly. And we’re talking about Blizzard! A company that spends years meticulously honing its games for the optimal playing experience, one of the few companies that actually conducts rigorous research for these sorts of issues. If Blizzard can’t do it right, who can?

Since I’m not stereoscopically normal (neither is Penny Arcade’s Mike Krahulik, apparently), I went out of my way to ask other people at the show how they felt about 3D. Most people at the NVIDIA booth seemed unimpressed. They complained about the subtlety of the 3D effect, the dimness of the images, eye strain, the inability to spectate if you weren’t wearing 3D glasses, and the general awkwardness of these systems. People were more positive when asked about the Nintendo 3DS, which makes a certain amount of sense, as Nintendo’s system is much less cumbersome and produces brighter images.

So that’s the shape of 3D: a wasteland of finicky technology, dark, muddled images, and uncomfortable customers who can barely manage to feign enthusiasm for the duration of a show, let alone hours in the living room. That kid playing World of Warcraft? He wasn’t playing it because it was 3D. He was playing it because he loves World of Warcraft. If 3D is to have any kind of future, it needs to create compelling experience that you can’t get in 2D, and I’m not sure that such a thing is possible.

During my hours in the exhibition hall, I also caught Ubisoft’s Child of Eden. More accurately, it caught me, as well as everyone else who passed within sight of it. Child of Eden looks like something out of the year 2045, a rhythm-based first person shooter that relies on the Xbox Kinect for interaction. Players fly through the game’s trippy environments simply by waving their hands. I didn’t get a chance to play it for myself, but even as a spectator, the experience is incredibly immersive. The flowing visuals and organic pace of action are mesmerizing, and seeing players control the game without a physical controller was downright arresting. An awe-inspiring piece all around, and not a 3D goggle in sight.

The books have closed on Child’s Play 2010, and this year’s total is a truly awe-inspiring 2.3 million dollars. With 2010 in the total, this means that cumulatively, Child’s Play has raised just shy of nine million dollars. Nine million dollars over the last eight years, every single cent of it helping to improve the life of a sick kid. If that’s not something to be proud of, I don’t know what is.

But I didn’t sit down in front of the computer today to talk to you about that. I do that enough. Instead, we’re going to talk about this sweet chart I made. Incidentally, at the time of this writing, Googling “sweet chart I made” returns this as the first result. Who am I to disagree?

Last year’s chart was put together with Numbers. I’m generally very happy with Numbers—certainly much happier than I ever was with the sluggish, bloated, obtuse mess that is Microsoft Excel—but the chart I produced last year has some problems. The spacing on the x-axis looks weird, and that’s a poor way to format a date anyway. Since the key shows the annual totals, it kind of defeats the point of the chart. And why did I go with a filled line chart? Because every year has many missing data points, and a filled chart was the only way to get Numbers to draw each year as a connected line.

This year’s chart was put together with R and ggplot2. Here’s what I like about it, and what I don’t.

What I Like

• R and ggplot2. I can’t recommend R highly enough. It’s fast, flexible, powerful, and oh yeah, free. I now use it for all my data analysis needs. I intentionally gave myself a hellish, badly formatted CSV file to work with here, just to see if R could beat it into shape. No sweat. As for ggplot2, it’s overkill for some situations, but a great solution for most. Maps, anyone?
• The date axis. It’s nicely labeled, with every major gridline representing exactly one week. Look closely, and you’ll see that the minor gridlines split the weeks into days.
• I ditched the legend, and instead placed year labels at the ends of their respective lines. Extra special audience challenge: do this in Excel without killing yourself after fifteen minutes.
• Cumulative total is computed on the fly and automatically added to the plot’s title.
• In fact, the whole plot is defined programmatically, even the year labels, so adding in 2011’s data should be a cinch.

What I Don’t Like

• There are too many colors on this thing. ggplot2 computes those colors by finding equally spaced points along the rainbow, so as more colors are added, the difference between them gets smaller. I’m using these colors to keep each line visually separate, but why? Do you need to see every data point of every year? One alternative would be to color in the current year and the previous year, and turn all others a shade of dark gray.
• The larger problem, though, is that this plot doesn’t serve much of a point. I don’t have enough data to get an accurate sense of how quickly Child’s Play accumulates funds. Look at where the lines start. The early years start at $0, but the spread runs up to nearly $500,000. Is that variability a reflection of larger corporate donations kicking off the fundraiser, or is it that Child’s Play runs year-round, and the charity is taking more money in during the non-holiday months of the year? In short, the only reliable data points in the plot are the totals, in which case a simple table could tell you just as much.

Still, it’s a fun exercise. I certainly learned a lot about R while working on this, and that’ll pay off in the future. Maybe I’ll tackle Boston’s weather data instead.

I became a published author as of a few weeks ago! The paper is titled “Perceptual learning of oriented gratings as revealed by classification images”, which is…a mouthful. Don’t get me wrong, I’m very proud of this. Designing the experiment, collecting the data, and writing the paper all added up to a tremendous learning experience, and the final product is a solid piece of work. Still, it’s not exactly beach reading. So, herein and forthwith, a plain-English explanation of this thing I just published. Yes, you too can understand science!

Before you can really understand what this paper is about, you need to understand perceptual learning. I’ve talked about this before, but here’s another quick primer. Learning of any sort requires practice, whether the goal is to recite all 50 state capitals from memory, ride a unicycle, or perhaps most interestingly, do both at once. In these examples, learning involves the parts of your brain that handle memory, motor skills, or both. Likewise, practice can also change the parts of your brain responsible for vision. When you perform a difficult visual task again and again (like, say, a dentist looking for cavities or a hunter looking for deer), the neurons responsible for processing this visual information become more refined, better at representing the important aspects of the task. It’s not that you simply understand what you’re looking at in a different way (which would be a change in strategy), it’s that you are literally getting better at seeing. Perceptual learning can enable a person to detect tiny changes in an object’s position, make a person more sensitive to detecting motion, enhance contrast sensitivity, and many other things.

So how do we measure perceptual learning? Typically we’ll sit you down in a dark, quiet room and give you a difficult visual task to do. At first you probably won’t be very good, and your answers will be random. But after making thousands of these visual decisions over several days, you will get better at it, and we’ll be able to measure that improvement. Usually we’ll boil all these trials down to a simple summary, like percent correct. The point is that we’ll sit you down for an hour at a time and have you complete 1,000 trials of an experiment, and out of all that data we’ll extract perhaps a handful of useful numbers.

This very common approach comes with some limitations. First, it seems a bit wasteful to sit someone down for a full hour and have only a few useful numbers to show for it. More importantly, though, remember that I’m using your behavior (how well you do on the task) to draw conclusions about what’s going on in your brain. This is problematic, because while I can see that you’re learning the task, I can’t say what, exactly, is being learned. This is one of the major debates in the field. Are you getting better at the task because your brain is becoming more sensitive to the important parts of the task, or because your brain is getting better at filtering out the parts that don’t matter?

Suppose that instead of walking away with a handful of numbers, I was able to produce an image from your data, a picture of the mental template you were using as you performed the task. To get an idea of what I mean, look at these images from a 2004 paper by Kontsevich and Tyler, charmingly titled, “What makes Mona Lisa smile?” The researchers were interested in what aspects of the Mona Lisa’s face influence her famously ambiguous smile. To answer this question, Kontsevich and Tyler took a picture of the Mona Lisa and then added what we call “visual noise,” basically frames of TV static. As you can see from the black and white images, the random noise alters the Mona Lisa’s expression in various small ways. Participants in the study were simply asked to classify whether all these different Mona Lisas looked happy or sad. Once that was done, all of the noise that was classified as making the Mona Lisa “happy” could be averaged together and then laid back on top of Mona Lisa, producing a “happy” Mona Lisa (right color image). Ditto all the “sad” noise, producing a sad Mona (left color image). The basic message? The mystery of Mona Lisa is all in the mouth.

Kontsevich and Tyler managed to produce these classification images very efficiently by layering the noise on top of the picture. But if you wanted to produce a classification image of the Mona Lisa purely from noise, you would need tens of thousands of trials before you started to get something that looked like a woman’s face. This presents a problem for those of us who study perceptual learning, because we usually like to examine how perceptual learning takes shape over the course of a few days. Therefore, we need a way to produce a good classification image purely from noise, and out of one hour’s worth of data. That way we can examine how the image changes day to day.

That’s really the whole point of our paper here: can we find a way to make good classification images from very little data, and if so, can we then analyze the classification image to figure out what, exactly, is changing as perceptual learning occurs?

We decided to apply this concept to a pretty classic task in the perceptual learning field: the detection of an oriented grating in noise. Oriented grating is just another way of saying “tilted stripe”. An hour a day for 10 training days, we’ll have you look at stimuli that are either 100% noise, or a mixture of noise and grating. The grating is always tilted to the same angle, until day 11, when we rotate everything 90 degrees (we call this the transfer session, since we want to see if your learning transfers to a grating of a different angle). In the image below, you see, from left to right, the training grating, the transfer grating, an example of what pure noise looks like, and an example of a noise/grating mixture.

The trick to producing classification images from small amounts of data is to simplify your stimuli as much as possible. In most studies gratings look more like the image at the left, but in our study we’ve eliminated all shades of gray, and kept our stimuli very low-resolution. Each stimulus is just 16x16 pixels, but blown up to about the size of a Post-it note on the screen. This way, instead of each stimulus being composed of several thousand pixels and several hundred colors, ours have just 256 pixels and two colors.

And it works! Here are classification images from one of our subjects for Day 1, Day 10, and the Transfer Day (“T”). As you can see, the classification image is fairly indistinct on Day 1, shows a much clearer stripe pattern by Day 10, and then gets worse again when the orientation is changed for the Transfer session (all images have been rotated to the same orientation for ease of comparison). In case the effect still isn’t clear, the right column applies some extra filtering to the images in the left to enhance the effect. And remember, while all our stimuli used only black or white pixels, the classification images have shades of gray because they represent an averaging of all those stimuli.

Our next hurdle was how, exactly, to measure the “goodness” of each classification image. Our solution was to calculate the Pearson correlation between each classification image and the target grating. In other words, a fairly straightforward measure of how well these two pictures match up, with 1.0 being a perfect score. Once you have that, you can see how the correlations change over time. In our data, image quality clearly improves for about six days, and then levels off. When we change the orientation of the target grating, performance drops back to square one:

My more eagle-eyed readers might notice something ironic about all this. Did we just go through all this trouble to create a classification image, only to convert the image back to a simple number again? But wait, there’s more. What if I created a grating at every possible orientation, and then calculated how well a person’s classification image correlated with each of those? I end up with what we call a tuning function. Ordinarily you can only get those if you’re plugging wires into animals’ brains and directly measuring the activity of their neurons. But have a look:

The red line represents the tuning function for Day 10 classification images. See where the red line intersects with the line labeled “45°”? That’s the equivalent of the Day 10 data point in the previous figure. But because I’ve gone through the trouble of creating this classification image and measuring its correlation with 180 different gratings, I can see much more than a single data point. I can see that there’s a big improvement immediately around the orientation that was trained, but that this improvement rapidly drops off as you move farther from it. In fact, most of the red line is below zero, indicating that the fit between the classification image and these other gratings has actually decreased, or been inhibited.

Then there’s the blue line, which represents the tuning function for Transfer Day. Its spike is 90 degrees away from the red line’s, which you’d expect. But the spike is also smaller and broader, indicating that learning to detect one grating transfers imperfectly to others. Also of interest, you might notice that the blue line has a noticeable “bump” near the spike of the red line. This suggests that even when subjects are told to search for this new Transfer grating, they are using a mental template that is tuned for what they had been trained on previously.

Lastly, no two people are ever going to produce identical classification images, which makes the images useful for revealing individual differences and strategies. Early on in this study, we noticed that some subjects produced very nice-looking images and showed very clear learning trends. Others seemed to produce murkier images and flat or even reversed learning effects (they seemed to get worse over time, not better). What to do with subjects like this is always a thorny question. So, we split the subjects into two groups: learners and non-learners. We found, somewhat surprisingly, that the so-called “non-learners” actually started off with better images than the “learners,” but that they never seemed to improve beyond their starting point. Our analyses showed that the non-learners tended to focus on the center of the stimuli. Their classification images looked like bright blobs, not stripes. It’s a perceptual strategy that worked well for them initially, but failed to generate measurable learning. Meanwhile, the learners started off a bit worse, but seemed to incorporate more of the stimulus into their decisions, and thus produced better classification images. In other words, the non-learners were lazy, and we were able to see and quantify this thanks to the classification images.

That, ladies and gentlemen, is the story: an efficient way to pull a picture out of a person’s brain, and what that picture can tell us about how that person learns. In closing, I’d like to point out that this thing didn’t spring fully formed from our minds. It was accepted for publication as of October, but for three years before that it was a work in progress. More than that, it was one huge learning experience for me. How to program the stimuli, how to design the experiment so that subjects don’t fall asleep in the middle of it, how to detect a cheater, how to analyze the data, how to slice and dice the data, how to ask questions, how to get answers, how to write it up, and how to handle the revisions, all of this was a a learn-on-the-job deal. I’d particularly like to thank my advisor on this project, Aaron Seitz, for all his help and guidance.